逐次反応の中間状態について-01

逐次反応に関しては，ここ，に３状態の場合を記載しました．

しかし，複数のステップの場合はどのように各状態の時間変化を考えればいいのでしょう？

\( \Large \ce{A_0 ->C[k] A_1->C[k ] A_2->C[k ] \cdots ->C[k ] A_{n-1} ->C[k ] A_n } \)

上記の反応の場合の各状態の時間変化を考えていきましょう．

ここで，

\( \Large \displaystyle \sum_{i=0}^n A_i =1 \)

とします．

・A₀

\( \Large \frac{dA_0}{dt} = -kA_0 \)

なので，これは簡単に，

\( \Large A_0 = e^{-kt} \)

となります．

・A₁

\( \Large \begin{eqnarray} \frac{dA_1}{dt} &=& -kA_1 + k A_0 \\
&=& -kA_1 + ke^{-kt} \\
\end{eqnarray} \)

なので，これは，ここ，を使って，

\( \Large A_1 = e^{-kt} (kt + C) \)

初期条件では，t=0, A₁=0,　なので

\( \Large A_1 = kte^{-kt} \)

となります．

・A₂

\( \Large \begin{eqnarray} \frac{dA_2}{dt} &=& -kA_2 + k A_1 \\
&=& -kA_2 + k^2te^{-kt} \\
\end{eqnarray} \)

なので，これは，ここ，を使って(m=1)，

\( \Large A_2 = e^{-kt} (\frac{1}{2}k^2t^2 + C) \)

初期条件では，t=0, A₂=0,　なので

\( \Large A_2 = \frac{1}{2}k^2t^2 e^{-kt} \)

となります．

・A₃

\( \Large \begin{eqnarray} \frac{dA_3}{dt} &=& -kA_3 + k A_2 \\
&=& -kA_3 + \frac{1}{2}k^2t^2 e^{-kt} \\
\end{eqnarray} \)

なので，これは，ここ，を使って(m=2)，

\( \Large A_3 = e^{-kt} (\frac{1}{2} \frac{1}{3}k^3t^3 + C) \)

初期条件では，t=0, A₃=0,　なので

\( \Large A_3 = \frac{1}{2 \times 3}k^3t^3 e^{-kt} \)

となります．

・A_n-1

ここまでくると法則性がわかりますので，m=n-1，の場合には，

\( \Large A_{n-1} = \frac{1}{(n-1)!}k^{n-1}t^{n-1} e^{-kt} \)

となります．

・A_n

nの場合は，その後に続く反応がありませんので，上の法則は成り立ちません．

しかし，ガンマ分布，でもお示ししましたように，

\( \Large P(x) = \frac{x^{\alpha-1} exp^{-x \theta}}{ \Gamma ( \alpha) \theta^{\alpha}} \)

となります．上記反応式の記号に書き換えると(nを整数として），

\( \Large P(t) = \frac{k^n t^{n-1} e^{-kt}}{ (n-1)!} \)

となります，これは，時刻ｔにおける確率密度なので，累積密度関数にして，

\( \Large A_n =\displaystyle \int_{0}^{ t } \frac{k^n t'^{n-1} e^{-kt'}}{ (n-1)!} dt' \)

となります，しかし，この積分は解析的にはややこしい式となるので，

\( \Large A_n = 1- \displaystyle \sum_{i=0}^{n-1} A_i \)

としてもいいのかもしれません．

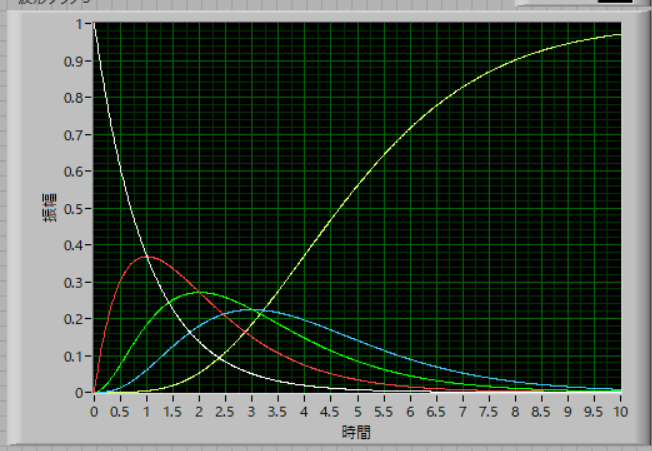
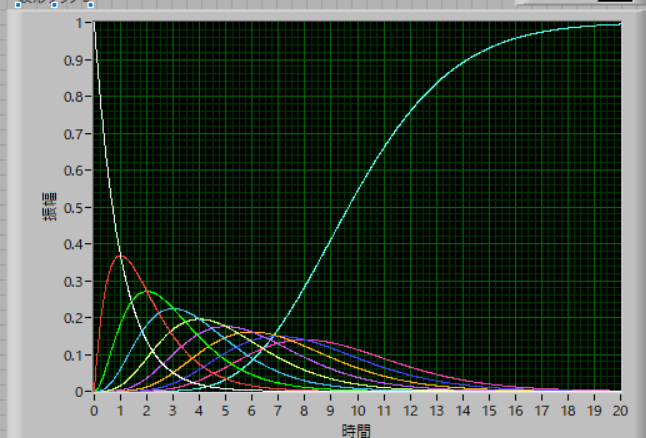
実際の時間変化

実際の時間変化は，

n=4

n=10

のようになります．